Definisi Eigenvalues dan Eigenvector

rumus dasar : $\( A v =\lambda v \)$

Eigenvector adalah vektor yang arahnya tidak berubah ketika dikalikan dengan matriks \(A\), hanya diperbesar atau diperkecil.

Eigenvalue adalah faktor pengali skalar yang menunjukkan seberapa besar eigenvector diperbesar atau diperkecil oleh matriks \(A\).

mencari eigenvalues eigenvector

Diberikan matriks:

\[\begin{split} A = \begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix} \end{split}\]

Langkah 1: Mencari Eigenvalue (\(\lambda\))

Kita gunakan rumus:

\[ \det(A - \lambda I) = 0 \]

\[\begin{split} A - \lambda I = \begin{bmatrix} 4 - \lambda & 2 \\ 1 & 3 - \lambda \end{bmatrix} \end{split}\]

\[ \det(A - \lambda I) = (4 - \lambda)(3 - \lambda) - (1)(2) \]

\[ = (12 - 4\lambda - 3\lambda + \lambda^2) - 2 = \lambda^2 - 7\lambda + 10 \]

Selesaikan persamaan kuadrat:

\[ \lambda^2 - 7\lambda + 10 = 0 \Rightarrow (\lambda - 5)(\lambda - 2) = 0 \]

Maka diperoleh eigenvalue:

\[ \lambda_1 = 5, \quad \lambda_2 = 2 \]

---

Langkah 2: Mencari Eigenvector (\(\vec{v}\))

---

Untuk \(\lambda = 5\):

\[\begin{split} A - 5I = \begin{bmatrix} -1 & 2 \\ 1 & -2 \end{bmatrix} \end{split}\]

Kita cari solusi dari:

\[\begin{split} (A - 5I)\vec{v} = \vec{0} \Rightarrow \begin{bmatrix} -1 & 2 \\ 1 & -2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{split}\]

Ambil persamaan dari baris pertama:

\[ -1x + 2y = 0 \Rightarrow x = 2y \]

Misal \(y = 1 \Rightarrow x = 2\)

Jadi, salah satu eigenvector-nya:

\[\begin{split} \vec{v}_1 = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \end{split}\]

---

Untuk \(\lambda = 2\):

\[\begin{split} A - 2I = \begin{bmatrix} 2 & 2 \\ 1 & 1 \end{bmatrix} \end{split}\]

Selesaikan:

\[\begin{split} (A - 2I)\vec{v} = \vec{0} \Rightarrow \begin{bmatrix} 2 & 2 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{split}\]

Ambil dari baris kedua:

\[ x + y = 0 \Rightarrow x = -y \]

Misal \(y = 1 \Rightarrow x = -1\)

Maka:

\[\begin{split} \vec{v}_2 = \begin{bmatrix} -1 \\ 1 \end{bmatrix} \end{split}\]

---

Hasil Akhir:

• \(\lambda_1 = 5\) dengan eigenvector \(\vec{v}_1 = \begin{bmatrix} 2 \\ 1 \end{bmatrix}\)

• \(\lambda_2 = 2\) dengan eigenvector \(\vec{v}_2 = \begin{bmatrix} -1 \\ 1 \end{bmatrix}\)

import numpy as np
A = np.array([[4, 2],
              [1, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print("Eigenvalue:")
print(eigenvalues)

print("\nEigenvector (setiap kolom adalah eigenvector):")
print(eigenvectors)

Eigenvalue:
[5. 2.]

Eigenvector (setiap kolom adalah eigenvector):
[[ 0.89442719 -0.70710678]
 [ 0.4472136   0.70710678]]

import numpy as np
import matplotlib.pyplot as plt

# Matriks A
A = np.array([[4, 2],
              [1, 3]])

# Hitung eigenvalue dan eigenvector
eigenvalues, eigenvectors = np.linalg.eig(A)

# Titik asal (0, 0) untuk setiap vektor
origin = np.array([[0, 0], [0, 0]])  # shape (2,2)

# Siapkan vektor
vec1 = eigenvectors[:, 0]  # eigenvector 1
vec2 = eigenvectors[:, 1]  # eigenvector 2

# Plotting
plt.figure(figsize=(6, 6))
plt.axhline(0, color='gray', lw=1)
plt.axvline(0, color='gray', lw=1)
plt.grid()
plt.gca().set_aspect('equal')

# Plot eigenvectors (biru)
plt.quiver(*origin, [vec1[0], vec2[0]], [vec1[1], vec2[1]], color=['blue', 'blue'], scale=1, scale_units='xy', angles='xy', label='Eigenvectors')

# Plot hasil transformasi A*v (merah)
Av1 = A @ vec1
Av2 = A @ vec2
plt.quiver(*origin, [Av1[0], Av2[0]], [Av1[1], Av2[1]], color=['red', 'red'], scale=1, scale_units='xy', angles='xy', alpha=0.6, label='A * v')

# Label dan legenda
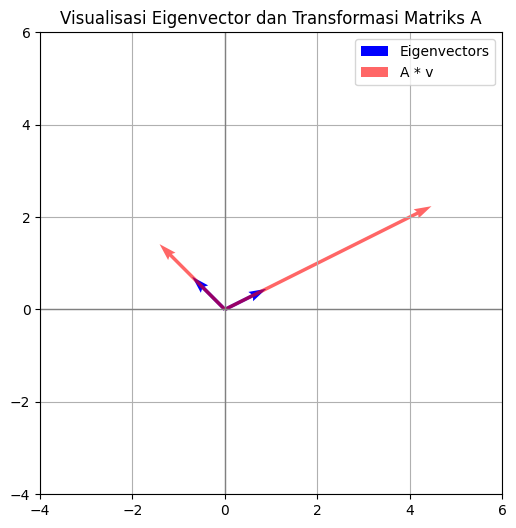
plt.title("Visualisasi Eigenvector dan Transformasi Matriks A")
plt.xlim(-4, 6)
plt.ylim(-4, 6)
plt.legend()
plt.show()

Ortonormal dan Ortogonal

definisi ortonormal dan ortogonal :

ortonormal adalah himpunan vektor yang saling ortogonal (tegak lurus) dan masing-masing memiliki panjang (norma) 1.

ortogonal adalah “saling tegak lurus” atau “membentuk sudut siku-siku”

menjadikan eigenvector menjadi satu satuan

code dibawah ini merupakan ortonormal karena jika ditambahkan masing-masing eigenvector nya memiliki panjang 1

import numpy as np
A = np.array([[4, 2],
              [1, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print("Eigenvalue:")
print(eigenvalues)

print("\nEigenvector (setiap kolom adalah eigenvector):")
print(eigenvectors)

Eigenvalue:
[5. 2.]

Eigenvector (setiap kolom adalah eigenvector):
[[ 0.89442719 -0.70710678]
 [ 0.4472136   0.70710678]]